Woah! TensorFlow! Neural Networks! Convolutionation Recurrent Deep Learned Blockchain Etherium Network. Where’s the line start??

Okay, maybe the last one isn’t actually a thing (for all I know). But there is currently a lot of hype and excitement around deep learning, and for good reason. Neural networks have provided a number of improvements in performance, and specific fields such as computer vision, speech recognition, and machine translation have been genuinely revolutionized by deep learning.
With that said, this will be Part 1 of the Grind my Gears series, where I will be talking about Deep Learning issues that just really grind my gears. This will be a less mathematic post than usual, but I will link to resources to dive in deeper if you are interested. With that said, let us begin:
SCREW OPTIMIZATION:
In deep learning, particularly very deep neural networks, you don’t want to optimizer the loss function ..
.

You heard me right. Think about it. Starting at about 10 parameters, a logistic regression model is will begin to perform better on training data than test data. This means that a logistic regression model is overfitting the training data. Now, take a typical deep learning model, with millions and millions of parameters to fit. At this absurd level of dimensionality, it is actually possible to perfectly fit the training data. This is the reason why, in Deep Learning, train/test curves like this are extremely common:
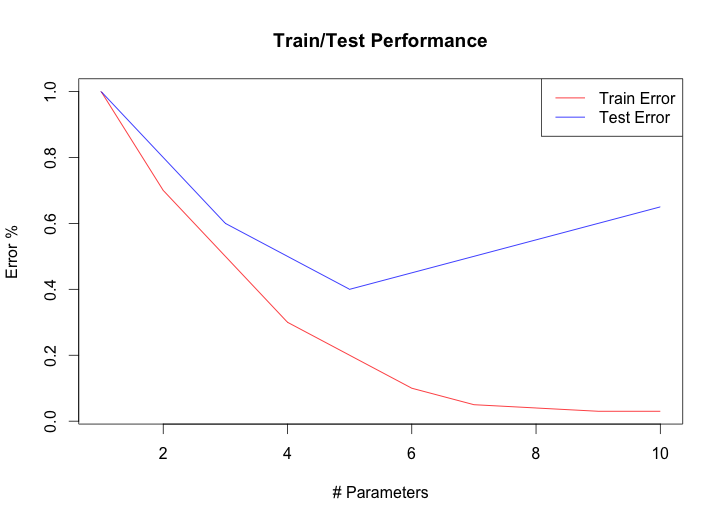
Finding the global minimum of loss function equivalent to literally memorizing a training set. It’s like a magic trick: Give me a Deep CNN network, and a couple hundred hours of GPU time, and I can turn it into a K Nearst Neighbors Algorithm.
The Adam Optimizer
And now we get to our optimizers. In this post, I talk about the benefits of second order optimizers over first order optimizers. Essentially the idea is that, a second order optimizer such as BFGS will account for not only the gradient, but also the rate at which the gradient is changing. As a result of this, second order optimizers are much faster and are guaranteed to approach local minima, and avoid saddle points.
However, first order optimizers can approximate second order optimizers by taking a small enough step size. This is why training step sizes are sooo small and why they take sooooo long. In order to speed up training and improve robustness, a number of new ‘momentum based’ optimizers have arisen, the most prominent of them being Adam. If you want to read more on Adam, check out this link. These optimizers have been gaining a lot of traction in the Deep Learning community and seem to provide excellent results. However, in a recent paper, it was shown that the Adam optimizer is actually worse at optimizing the loss function than even basic SGD.
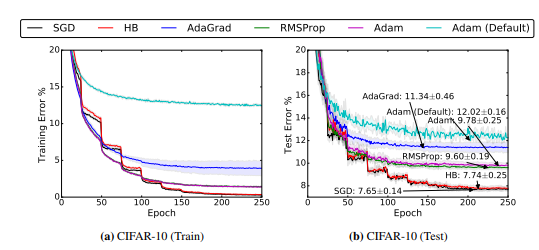
However, throughout the endless iterations and trial and error of industry, it’s been clearly demonstrated that there’s something magical about that combination of ‘Relu’+Dropout+’Adam’ that just works magic. And it seems like part of that magic is in failing to optimize loss functions.
The line of logic that most resonates me has to do with optimization spaces. Say you have 2 global minima for your loss function: one that is broad and local, and one that is sharp and global. Take the figure below for example:
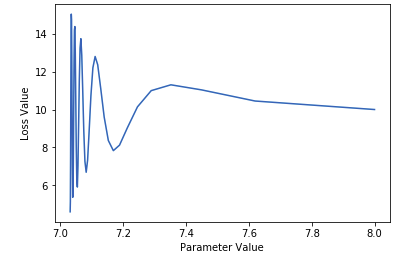
There is a sharp global minimum at 7.0, but at 7.2, there is a much broader local minimum at 7.2. An extremely robust optimizer, after enough iterations, should be able to find the global minimum. However, it may actually be that case that we don’t want these sharp maxima even if they provide a lower training loss that the previous point. A sharp probabilistic point such as the one at X=7.0, is extremely unstable, since any fluctuation of your values (or, perhaps, of your data), could cause it’s accuracy to crash. However, ending on a much broader, albeit lower, optimization point, is almost akin to ensembling a model, since, you are not only providing that single Maximum likelihood estimate of the parameters, but also a solid estimate of the broad minimum around it.
Remember, a neural networks is capable of memorizing the training data, so it would make a lot of sense, at least to me, that these broad local minima are really what allows neural networks to generalize. And that may be why the Adam optimizer, even though it consistently performs “Worse” than even SGD, seems to provide better performance.
Now let’s just take a step back and evaluate how backwards this is. The typical paradigm in machine learning is that you have some training data that you want to fit, and hopefully, you use an algorithm that fits your data in such a way that you are able to find generalized trends. However, in the backwards world of deep learning, we have this model that is so flexible, so robust, that it seems our goal is to actually prevent our model from optimizing the function that we are trying to optimize.

So that’s my first post of my current issues in the field of deep learning. Hope this shed a little light on why people continually refer to Deep Learning as a black box, where up is down, good is bad, and loss is good for accuracy. Stay tuned for the next post. Hope ya’ll enjoyed!
